Page 102 - Mešinovič, Sanela, Mara Cotič, Amalija Žakelj. 2019. Učenje in poučevanje geometrije v osnovni šoli. Koper: Založba Univerze na Primorskem.
P. 102
enje in poučevanje geometrije
P T E
B A, G E, F, H
C, D P
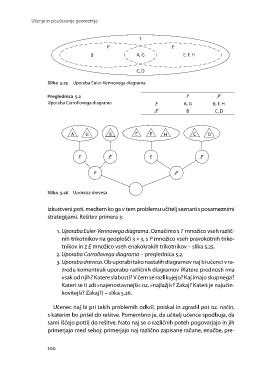
Slika 5.25 Uporaba Euler-Vennovega diagrama A, G
Preglednica 5.2 E B P
Uporaba Carrollovega diagrama E E, F, H
C, D
AG B E FH CD
EE EE
P P
Slika 5.26 Uporaba drevesa
izkustveni poti, medtem ko ga v tem problemu učitelj seznani s posameznimi
strategijami. Rešitev primera 3:
1. Uporaba Euler-Vennovega diagrama. Označimo s T množico vseh različ-
nih trikotnikov na geoplošči 3 × 3, s P množico vseh pravokotnih triko-
tnikov in z E množico vseh enakokrakih trikotnikov – slika 5.25.
2. Uporaba Carrollovega diagrama – preglednica 5.2.
3. Uporaba drevesa. Ob uporabi tako nastalih diagramov naj bi učenci v ra-
zredu komentirali uporabo različnih diagramov (Katere prednosti ima
vsak od njih? Katere slabosti? V čem se razlikujejo? Kaj imajo skupnega?
Kateri se ti zdi »najenostavnejši« oz. »najlažji«? Zakaj? Kateri je najučin-
kovitejši? Zakaj?) – slika 5.26.
Učenec naj bi pri takih problemih odkril, poiskal in zgradil pot oz. način,
s katerim bo prišel do rešitve. Pomembno je, da učitelj učence spodbuja, da
sami iščejo pot(i) do rešitve. Nato naj se o različnih poteh pogovarjajo in jih
primerjajo med seboj: primerjajo naj različno zapisane račune, enačbe, pre-
100
P T E
B A, G E, F, H
C, D P
Slika 5.25 Uporaba Euler-Vennovega diagrama A, G
Preglednica 5.2 E B P
Uporaba Carrollovega diagrama E E, F, H
C, D
AG B E FH CD
EE EE
P P
Slika 5.26 Uporaba drevesa
izkustveni poti, medtem ko ga v tem problemu učitelj seznani s posameznimi
strategijami. Rešitev primera 3:
1. Uporaba Euler-Vennovega diagrama. Označimo s T množico vseh različ-
nih trikotnikov na geoplošči 3 × 3, s P množico vseh pravokotnih triko-
tnikov in z E množico vseh enakokrakih trikotnikov – slika 5.25.
2. Uporaba Carrollovega diagrama – preglednica 5.2.
3. Uporaba drevesa. Ob uporabi tako nastalih diagramov naj bi učenci v ra-
zredu komentirali uporabo različnih diagramov (Katere prednosti ima
vsak od njih? Katere slabosti? V čem se razlikujejo? Kaj imajo skupnega?
Kateri se ti zdi »najenostavnejši« oz. »najlažji«? Zakaj? Kateri je najučin-
kovitejši? Zakaj?) – slika 5.26.
Učenec naj bi pri takih problemih odkril, poiskal in zgradil pot oz. način,
s katerim bo prišel do rešitve. Pomembno je, da učitelj učence spodbuja, da
sami iščejo pot(i) do rešitve. Nato naj se o različnih poteh pogovarjajo in jih
primerjajo med seboj: primerjajo naj različno zapisane račune, enačbe, pre-
100